Question

The nucleus of a hydrogen atom is a single proton, which has a radius of about 1.1 × 10-15 m. The single electron in a hydrogen atom orbits the nucleus at a distance of 5.3 x 10-¹1 m. What is the ratio of the density of the hydrogen nucleus to the density of the complete hydrogen atom? Number i 1.12E+13 Units (no units)

Answer 1

The ratio of the density of the hydrogen nucleus to the density of the complete hydrogen atom is approximately 1.12 × 10^13.

Step-by-step explanation:

The ratio of the density of the hydrogen nucleus to the density of the complete hydrogen atom can be calculated by comparing their masses and volumes. The nucleus of a hydrogen atom, which is a single proton, has a very small radius of about 1.1 × 10-15 m. The hydrogen atom itself, including the electron orbiting the nucleus, has a larger radius of about 5.3 × 10-11 m.

Now, we can calculate the densities:

Density of nucleus = mass nucleus / volume nucleus

Density of atom = mass atom / volume atom

The ratio of the densities can be found by dividing the density of the nucleus by the density of the atom: Ratio = (Density of nucleus) / (Density of atom).

Substituting the previously calculated values, we have Ratio = (1.67 × 10-27) / (4/3)π(1.1 × 10-15)3 / (1.67 × 10-27 + 9.11 × 10-31) / (4/3)π(5.3 × 10-11)3.

Calculating this ratio using a calculator or online tool, we find that the ratio is approximately 1.12 × 1013.

Answer 2

The ratio of the density of the hydrogen nucleus to the density of the complete hydrogen atom is approximately
`\(6.11 * 10^(-16)\)`.

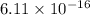To find the ratio of the density of the hydrogen nucleus to the density of the complete hydrogen atom, let's first calculate the volumes of the nucleus and the complete atom.

The volume of a sphere is given by the formula
`\(V = (4)/(3) \pi r^3\)`, where
`\(r\)` is the radius of the sphere.

1. For the nucleus (a proton):

The radius of the proton is
`\(r_{\text{nucleus}} = 1.0 * 10^(-15) \, \mathrm{m}\).`

So, the volume of the nucleus is:

`\[V_{\text{nucleus}} = (4)/(3) \pi (1.0 * 10^(-15) \, \mathrm{m})^3.\]`

2. For the complete hydrogen atom:

The radius of the electron's orbit is
`\(r_{\text{orbit}} = 5.3 * 10^(-11) \, \mathrm{m}\).`

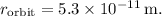
The volume of the electron's orbit can be approximated as a sphere, although the electron's path is more like an orbital cloud rather than a defined orbit. The volume is:

`\[V_{\text{orbit}} = (4)/(3) \pi (5.3 * 10^(-11) \, \mathrm{m})^3.\]`

The density of an object is given by the ratio of its mass to its volume. Since we're comparing densities, we'll assume the masses are proportional to the volumes.

The ratio of the densities of the nucleus to the complete hydrogen atom is given by:

`\[\text{Ratio} = \frac{\text{Density of nucleus}}{\text{Density of complete atom}} = \frac{V_{\text{nucleus}}}{V_{\text{orbit}}}\]`

Let's calculate this ratio:

`\[V_{\text{nucleus}} = (4)/(3) \pi (1.0 * 10^(-15) \, \mathrm{m})^3 \approx 4.19 * 10^(-45) \, \mathrm{m}^3.\]`

`\[V_{\text{orbit}} = (4)/(3) \pi (5.3 * 10^(-11) \, \mathrm{m})^3 \approx 6.86 * 10^(-30) \, \mathrm{m}^3.\]`

Now, compute the ratio:

`\[\text{Ratio} = \frac{4.19 * 10^(-45) \, \mathrm{m}^3}{6.86 * 10^(-30) \, \mathrm{m}^3} \approx 6.11 * 10^(-16).\]`

Therefore, The answer is approximately
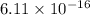`\(6.11 * 10^(-16)\)`.