Question

Write a coordinate proof. Given: Rectangle ABCD has vertices A(0,4), B(6,4), C(6,0), D(0,0). E is the midpoint of line DC. F is the midpoint of line DA. Prove: The area of rectangle DEGF is one fourth the area of rectangle ABCD.

Please help I've been trying for a while ​

Answer 1

The answer is below

Explanation:

Distance between two points
`A(x_1,y_1)\ and\ B(x_2,y_2)\ on \ the\ coordinate\ plane`

`|AB|=√((x_2-x_1)^2+(y_2-y_1)^2)`

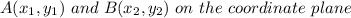
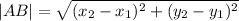
The area of rectangle = length * breadth

The area of rectangle ABCD = |AB| * |BC|

`|AB|=√((6-0)^2+(4-4)^2)=6\\\\|BC|=√((6-6)^2+(0-4)^2) =4`

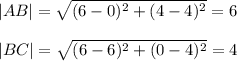
The area of rectangle ABCD = |AB| * |BC| = 6 * 4 = 24

E(x, y) is midpoint of line DC. Its coordinate is:

x = (6 + 0) / 2 = 3; y = (0 + 0) / 2 =0

The coordinate of E = (3, 0)

F(a, b) is midpoint of line DA. Its coordinate is:

a = (0 + 0) / 2 = 0; b = (4 + 0) / 2 = 2

The coordinate of E = (0, 2)

The area of rectangle DEGF = |DE| * |DF|

`|DE|=√((3-0)^2+(0-0)^2)=3\\\\|DF|=√((0-0)^2+(2-0)^2) =2`

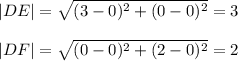
The area of rectangle ABCD = |DE| * |DF| = 3 * 2 = 6

Therefore, area of rectangle DEGF is one fourth the area of rectangle ABCD