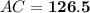Answer:
○
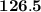
Explanation:
To solve this problem, we need to use the law of sines, which states that the ratios of the sines of angles and their opposite sides are equal for all angles inside a triangle.
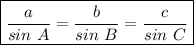 .
.
To use the law of sines to find a length, we need to have at least one angle whose measure and length of opposite side is known.
In this case, the only side whose length we know is BC = 85, but we don't know the measure of its corresponding angle (∠ A).
Let's find ∠ A:
∠ A + 85° + 53° = 180° [angles in a triangle add up to 180°]
⇒ ∠ A + 138° = 180°
⇒ ∠ A = 42°
Now we can use the law of sines to find the length of AC:
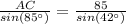
⇒
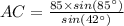
⇒