Question

Compute the value of the discriminant and give the number of real solutions of the quadratic equation.

−4x^2 + 6x - 1=0

Answer 1

Value of discriminant is 20

Explanation:

Formula of discriminant is:

`D=b^2-4ac`

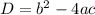
so our equation is

`-4x^2+6x-1=0`

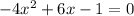
where a = -4, b = 6 , c = -1

so our discriminant becomes,

`D=b^2-4ac\\D=(6)^2-4(-4)(-1)\\D=36-16\\D=20`

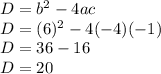
Since the discriminant is positive we have two distinct real number solutions or two distinct roots, and to solve the we just use the quadratic formula and get the two different values of x.

`x_1=0.191\\x_2=1.309`

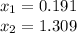
I have attached a graph also to confirm your answer, you use an online graphing calculator to verify it as well.