Answer: Time taken by Ximena to paint the fence alone = 24 hours
Time taken by Candice to paint the fence alone = 12 hours
Explanation:
Let x= Time taken by Ximena to paint the fence alone .
Time taken by Candice to paint the fence alone = x-12
As per given , we have
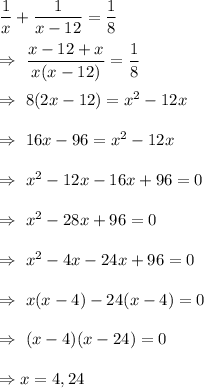
if x= 4
Time taken by Ximena = 4 hours
Time taken by Candice = 4-12 hours =-8 hours which is not possible. (time cannot be negative)
Therefore, x= 24
Such that
Time taken by Ximena to paint the fence alone = 24 hours
Time taken by Candice to paint the fence alone = 24-12=12 hours