Final answer:
The 99% confidence interval for the mean amount of all toll booth receipts is calculated using the formula for a large sample size and the z-score for a 99% confidence level. The resulting interval is ($8.84, $10.06).
Step-by-step explanation:
The question asks us to calculate the 99% confidence interval for the mean amount of all toll booth receipts based on a simple random sample. To compute the confidence interval for a mean, we use the formula:
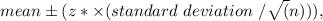 where z* is the z-score corresponding to the desired confidence level, standard deviation is the sample standard deviation, and n is the sample size. Since the sample size is over 30, we'll use the z-distribution which is appropriate for large samples according to the Central Limit Theorem.
where z* is the z-score corresponding to the desired confidence level, standard deviation is the sample standard deviation, and n is the sample size. Since the sample size is over 30, we'll use the z-distribution which is appropriate for large samples according to the Central Limit Theorem.
For a 99% confidence interval, the z-score is approximately 2.576. Thus, the confidence interval is calculated as
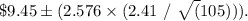
The computation yields the confidence interval as: $9.45 ± 0.61, or ($8.84, $10.06). We are 99% confident that the true mean of all receipts is between $8.84 and $10.06.