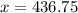Complete Question
Let x be a continuous random variable that follows a normal distribution with a mean of 550 and a standard deviation of 75.
a
Find the value of x so that the area under the normal curve to the left of x is .0250.
b
Find the value of x so that the area under the normal curve to the right ot x is .9345.
Answer:
a
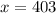
b
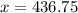
Explanation:
From the question we are told that
The mean is
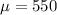
The standard deviation is
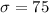
Generally the value of x so that the area under the normal curve to the left of x is 0.0250 is mathematically represented as
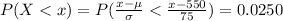
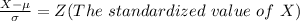
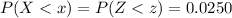
Generally the critical value of 0.0250 to the left is
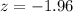
=>
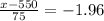
=>
![x = [-1.96 * 75 ]+ 550](https://img.qammunity.org/2021/formulas/mathematics/college/lntt9xxbgfpfetn682ddajprodw5m5nnuq.png)
=>
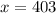
Generally the value of x so that the area under the normal curve to the right of x is 0.9345 is mathematically represented as
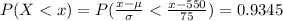
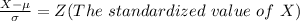
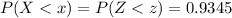
Generally the critical value of 0.9345 to the right is
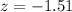
=>

=>
![x = [-1.51 * 75 ]+ 550](https://img.qammunity.org/2021/formulas/mathematics/college/m8uxxu6m25hyhjzsebt7sbyw6l5x1skz2w.png)
=>