Answer:
f(x) = 2x³ - 10x² - 34x + 42
Explanation:
The standard form of a cubic equation is f(x) = ax³ + bx² + cx + d
Given conditions are:
First: Zeros of the cubic function are - 3, 1, and 7
Second: f(- 2) = 54
a(-3)³ + b(-3)² + c(-3) + d = 0 ⇔ - 27a + 9b - 3c + d = 0 ...... (1)
a + b + c + d = 0 ......... (2)
a(7)³ + b(7)² + c(7) + d = 0 ⇔ 343a + 49b + 7c + d = 0 ....... (3)
a(-2)³ + b(-2)² + c(-2) + d = 54 ⇔ - 8a + 4b - 2c + d = 54 ...... (4)
We have 4 equations with 4 unknown variables.
Use Cramer's rule to solve the system
A =
![\left[\begin{array}{cccc}-27&9&-3&1\\1&1&1&1\\343&49&7&1\\-8&2&-2&1\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/u7i282andzifootiwvpac0xbz9jn0jw6ad.png) = 6,480
= 6,480
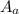 =
=
![\left[\begin{array}{cccc}0&9&-3&1\\0&1&1&1\\0&49&7&1\\54&2&-2&1\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/lzoqi7y2vbiiz4xtp6j55vtppns8p0swbs.png) = 12,960
= 12,960
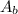 =
=
![\left[\begin{array}{cccc}-27&0&-3&1\\1&0&1&1\\343&0&7&1\\-8&54&-2&1\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/lb0w692s9loe6q8tbvtyp3oz94kczggc5u.png) = - 64,800
= - 64,800
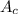 =
=
![\left[\begin{array}{cccc}-27&9&0&1\\1&1&0&1\\343&49&0&1\\-8&2&54&1\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/kreh0phiozmunj5l40u8c0t982kigtejxu.png) = - 220,320
= - 220,320
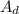 =
=
![\left[\begin{array}{cccc}-27&9&-3&0\\1&1&1&0\\343&49&7&0\\-8&2&-2&54\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/zy3qh3qtfgo13ywrsdlq2trjhvda8n6l84.png) = 272,160
= 272,160
a =
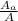 = 2
= 2
b =
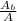 = - 10
= - 10
c =
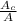 = - 34
= - 34
d =
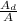 = 42
= 42
f(x) = 2x³ - 10x² - 34x + 42