Answer:
![\left[\begin{array}{ccc}3&-1&\\-1&1/2\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/k3l0z3m3md3gis74obzrpcwy2udihtgyk8.png)
Explanation:
The matrix system for the linear equations: x + 2y = 8, 2x + 6y = 9
![\left[\begin{array}{ccc}1&2&\\2&6\\\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] = \left[\begin{array}{ccc}8\\9\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/v1uatodq11or8986kp2sc0941s4vmvgy13.png)
To get the coefficient of x and y, the inverse of the first matrix (let the first matrix be A) must be known.
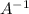 = (1 / determinant of A) x Adjoint of A
= (1 / determinant of A) x Adjoint of A
the determinant of A = (1 x 6) - (2 x 2) = 6 - 4 = 2
Adjoint of A =
![\left[\begin{array}{ccc}6&-2&\\-2&1\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/1jab44ftdxegaexabnh7a0je4g4zqyzhec.png)
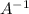 =
=
![(1)/(2) \left[\begin{array}{ccc}6&-2\\-2&1\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/oe3qm66n1sgm7bhy4v5t6gqxrzzfojk3mq.png) =
=
![\left[\begin{array}{ccc}3&-1&\\-1&1/2\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/k3l0z3m3md3gis74obzrpcwy2udihtgyk8.png)