Question

A parallelogram with coordinates A (-2,3), B (3,3), C (4,6), and D(-1,6) is the first rotated 90 degrees clockwise and then translated 4 units left and 2 units down to form quadrilateral A'B'C'D what is the distance, in units between point C' and point D' in the resulting figure

Answer 1

Given:

The vertices of a parallelogram are A (-2,3), B (3,3), C (4,6), and D(-1,6).

It is first rotated 90 degrees clockwise and then translated 4 units left and 2 units down to form quadrilateral A'B'C'D.

To find:

The distance between C' and D'.

Solution:

If a figure rotated 90 degrees clockwise, then

`(x,y)\to (y,-x)`

`C(4,6)\to C_1(6,-4)`

`D(-1,6)\to D_1(6,-(-1))=D_1(6,1)`

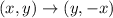
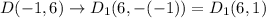
If figure translated 4 units left and 2 units down, then

`(x,y)\to (x-4,y-2)`

`C_1(6,-4)\to C'(6-4,-4-2)=C'(2,-6)`

`D_1(6,1)\to D'(6-4,1-2)=D'(2,-1)`

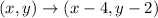
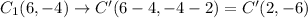
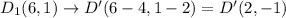
Distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

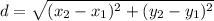
Distance between C'(2,-6) and D'(2,-1) is

`C'D'=√((2-2)^2+(-1-(-6))^2)`

`C'D'=√((0)^2+(-1+6)^2)`

`C'D'=√((5)^2)`

`C'D'=5`

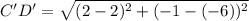
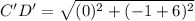
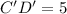
Therefore, the distance between C'D' is 5 units.