Question

Anya bought a car for £12 500.

The car depreciates at a rate of 12%
per year.
Work out the value of the car after
five years.

Answer 1

7500

Step-by-step explanation:

All you have to do is mulitiply the percent by 5 so 60% then you do 0.60 times 12500 to get 7500. Hope this helped!

Answer 2

After five years, the value of Anya's car will be £8,228.

Step-by-step explanation:

Anya's car depreciates at a rate of 12% per year. To calculate the depreciation over five years, we can use the formula for exponential decay:
`\[V_t = V_0 * (1 - r)^t\], where \(V_t\)` is the value after (t) years,
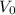`\(V_0\)` is the initial value, \(r\) is the rate of depreciation as a decimal, and (t) is the time in years.

In this case, Anya's initial investment
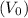`(\(V_0\))` is £12,500, the rate of depreciation (r) is 12% or 0.12, and the time (t) is 5 years. Plugging these values into the formula, we get:
`\[V_5 = £12,500 * (1 - 0.12)^5\]`

`\[V_5 = £12,500 * (0.88)^5\]`

`\[V_5 ≈ £8,228\]`

Therefore, after five years, the value of Anya's car will be approximately £8,228.

It's important to note that exponential decay models assume a continuous and constant rate of depreciation. In the context of this problem, it means that the car's value decreases by 12% each year without any fluctuations. This mathematical approach provides a straightforward method for calculating depreciation over time. Anya can use this information to estimate the future value of her car and plan accordingly for potential resale or replacement.