The equation of the line passing through the points (3,3) and (6,9), and also through the point (x, y), is
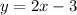 .
.
To find the equation of the straight line passing through the points (3,3) and (6,9), we can use the slope-intercept form of a line, which is given by:
![\[ y = mx + b \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/wtsqddmv4ciat8euuj6md8p7n5le92wt38.png)
where
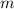 is the slope and
is the slope and
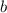 is the y-intercept.
is the y-intercept.
First, calculate the slope
 using the formula:
using the formula:
![\[ m = \frac{{y_2 - y_1}}{{x_2 - x_1}} \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/nrm5lebzeh5754i59xbqhlg6vkz3huz3ry.png)
Let
 :
:
![\[ m = \frac{{9 - 3}}{{6 - 3}} = (6)/(3) = 2 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/fsrohmch7i9zutfk03347slv52uoqoh9m9.png)
Now that we have the slope
 , we can use one of the points, say
, we can use one of the points, say
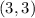 , to find the y-intercept
, to find the y-intercept
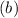 . Plug the values into the equation:
. Plug the values into the equation:
![\[ 3 = 2(3) + b \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/mzzaje9fc0sj0pq1nw7f2cgu91mlparrvp.png)
Solving for
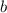 :
:
![\[ 3 = 6 + b \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/susq47th0gof124smndznv7authagu7ief.png)
![\[ b = 3 - 6 = -3 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/q9zzyrlcx08zr0488intz5hb62uawwupgk.png)
Now, we have the slope
 and the y-intercept
and the y-intercept
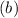 . The equation of the line is:
. The equation of the line is:
![\[ y = 2x - 3 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/nnu4nvx597emzvbx57cdh3i77cc2snl9n2.png)
Now, the line also passes through the point
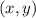 . Since this point lies on the line, we can substitute
. Since this point lies on the line, we can substitute
 and
and
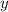 into the equation:
into the equation:
![\[ y = 2x - 3 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/nnu4nvx597emzvbx57cdh3i77cc2snl9n2.png)
This is the equation relating
 and
and
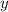 for the line passing through the points (3,3) and (6,9), as well as the additional point (x, y).
for the line passing through the points (3,3) and (6,9), as well as the additional point (x, y).
The question probable maybe:
All three points displayed are on the line. Find an equation relating x and y.