Answer:
Explanation:
we can find the equations for both lines and analyze after
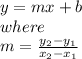
AB:
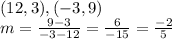
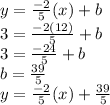
CD:
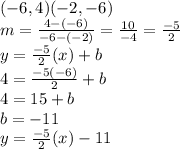
Determining whether two lines are parallel or perpendicular involves looking at their slopes. AB has a slope of -2/5, CD has a slope of -5/2. Since these are not equal (not parallel) and not negative reciprocals of each other (not perpendicular), the lines are neither perpendicular or parallel.