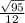Question

If the sinø=7/12, what is cosø?

Answer 1

If the sinø=7/12, cosø is
`(√(95) )/(12)`

Explanation:

We are given sinФ = 7/12

We need to find cosФ

The basic trigonometric functions of right triangle are:

`sin\theta=(opposite)/(hypotenuse)`

`cos\theta=(adjacent)/(hypotenuse)`

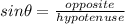
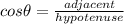
We need values of adjacent and hypotenuse to find cosФ

Using Pythagoras theorem we can find the value of adjacent

`(Hypotenuse)^2= (Opposite)^2+(Adjacent)^2`

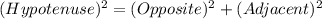
We have Hypotenuse= 12 and Opposite = 7 (because
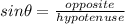`sin\theta=(opposite)/(hypotenuse)` and we are given
`sin\theta=(7)/(12)`

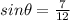
Inserting values and finding adjacent:

`(Hypotenuse)^2= (Opposite)^2+(Adjacent)^2\\(12)^2=(7)^2+(Adjacent)^2\\144=49+(Adjacent)^2\\144-49=(Adjacent)^2\\95=(Adjacent)^2\\√((Adjacent)^2) =√(95)\\Adjacent=√(95)`

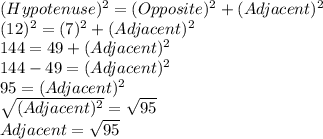
So, value of Adjacent is
`√(95)`

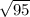
Now finding cosФ

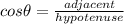
`cos\theta=(adjacent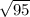)/(hypotenuse)`

Adjacent =
`√(95)`, hypotenuse = 12

`cos\theta=(√(95) )/(12)`

So, If the sinø=7/12, cosø is
`(√(95) )/(12)`