Question

Question Help

Reasoning A cone with radius 6 and height 9 has its radius quadrupled. How many times greater is the
volume of the larger cone than the smaller cone?l

Answer 1

Let's see

For initial cone

• r=6
• h=9

Volume

• 1/3πr²h
• 1/3π(6)²(9)
• 3(36)π
• 108π units³

For new cone

• r=4(6)=24
• h=9

Volume

• 1/3π(24)²(9)
• 3(576)π
• 1728π

So

• 1728π/108π
• 16times

Answer 2

16 times

Explanation:

`\textsf{Volume of a cone}=\sf (1)/(3) \pi r^2 h \quad\textsf{(where r is the radius and h is the height)}`

If only the radius is changed, the change in volume will be proportionate to the multiplicative factor squared.

`\sf \implies Volume =(1)/(3) \pi (ar)^2h=(1)/(3) \pi (a^2)r^2h`

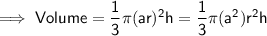
Therefore, if the cone is quadrupled (multiplied by 4), the volume of the larger cone will be 4² times greater than the volume of the smaller cone, so 16 times greater than the smaller cone.

Proof

Given:

• radius = 6
• height = 9

Substituting the given values into the formula:

`\sf \implies Volume =(1)/(3) \pi (6)^2(9)=108 \pi \: \:cubic\:units`

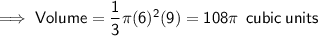
If the radius is quadrupled:

• radius = 6 × 4 = 24
• height = 9

Substituting the new given values into the formula:

`\sf \implies Volume =(1)/(3) \pi (24)^2(9)=1728 \pi \: \:cubic\:units`

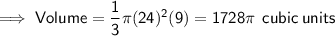
To find the number of times greater the volume of the large cone is than the volume of the smaller cone, divide their volumes:

`\sf \implies (V_(large))/(V_(small))=(1728\pi)/(108\pi)=16`

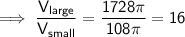
So the volume of the larger cone is 16 times greater than the volume of the smaller cone.