Triangle ABC is dilated by a scale factor of ⅜ to create triangle A'B'C'. The area of triangle ABC is u square units. What is the area of triangle A'B'C…

Question

asked Aug 11, 2021 53.0k views

1 Answer

Baloan · Answer 1 · 2021-08-15T19:01:06+0000

Given:

Triangle ABC is dilated by a scale factor of
(3)/(8) to create triangle A'B'C'.

To find:

The area of triangle ABC is u square units.

Solution:

Triangle ABC is dilated to create triangle A'B'C'. It means both triangles are similar.

We know that, the ratio of the areas of similar triangles is the square of the scale factor.

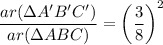
$(ar(\Delta A'B'C'))/(ar(\Delta ABC))=\left((3)/(8)\right)^2$

The area of triangle ABC is u square units.

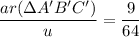
$(ar(\Delta A'B'C'))/(u)=(9)/(64)$

Multiply both sides by u.

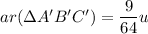
$ar(\Delta A'B'C')=(9)/(64)u$

Therefore, the area of triangle A'B'C' is
sq. units.