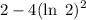Solution :
Let the distance of the stick from one break be X
And let us assume that
 .
.
Here, l = length of stick
Therefore,
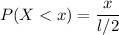
We know that,
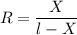 , so by definition we get
, so by definition we get

The cumulative distribution function for R is
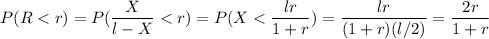
When it starts at zero, then r =0. It ends at one when the r has a maximum
value of one.
The probability density function is given by
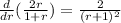
Now integrating, we find E(R) and
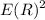 gives :
gives :
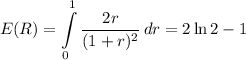

Therefore, Var(R)=