Answer:
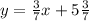
Explanation:
Slope-intercept form:
y= mx +c, where m is the gradient and c is the y-intercept.
Given equation: 7x +3y= 18
Rewrite into slope-intercept form to find out its gradient:
7x +3y= 18
3y= -7x +18
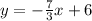
Thus, gradient of given line is -7/3.
The product of the gradients of 2 perpendicular lines is -1.
(Gradient of line)(-7/3)= -1
Gradient of line

Substitute m= 3/7 into the equation:

To find the value of c, substitute a pair of coordinates.
Since the line contains P(6,8), we substitute x=6 and y=8 into the equation.
When x=6, y= 8,

Thus, the equation of the line is
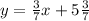 .
.