Question

Pls help me. this is inverse trigonometric function

Answer 1

I'll do the first problem to get you started.

In place of
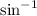`\sin^(-1)` I'll use arcsine

So
`\sin^(-1)(x) = \arcsin(x)`

-------------------------------------------------

Using that hint given, we can get the following

cos(arcsin(3x) - pi)

cos(arcsin(3x))*cos(pi) + sin(arcsin(3x))*sin(pi)

cos(arcsin(3x))*(-1) + sin(arcsin(3x))*(0)

-cos(arcsin(3x)) + 0

-cos(arcsin(3x))

Now the question is how to evaluate the cosine of an inverse trig function, especially when it's not inverse cosine.

The trick (often with many trig and geometry problems) is to draw out a triangle. Specifically we'll need a right triangle.

Check out the diagram below. I've drawn out a right triangle with reference angle theta, opposite leg of length 3x, and hypotenuse 1.

Note how sin(theta) = opposite/hypotenuse = 3x/1 = 3x

We can then go from sin(theta) = 3x to theta = arcsin(3x)

This ultimately means

cos(arcsin(3x)) = cos(theta)

cos(arcsin(3x)) = adjacent/hypotenuse

cos(arcsin(3x)) = sqrt(1-9x^2)/1

cos(arcsin(3x)) = sqrt(1-9x^2)

The sqrt(1-9x^2) is the result of using the pythagorean theorem.

---------------------------

So that means the final answer is
`-√(1-9x^2)`