Question

A circle has a diameter of 10 cm a square has a side length of 6 cm use Pythagoras Theorem to show that the square will fit inside the circle without touching the edge of the circle

Answer 1

Given:

Diameter of circle = 10 cm

Side length of square = 6 cm.

To show:

That the square will fit inside the circle without touching the edge of the circle.

Solution:

A square will fit inside the circle without touching the edge of the circle if the diagonal of the square is less than the diameter of the circle.

We have,

Side length of square = 6 cm.

Using Pythagoras theorem, the diagonal of the square is

`Hypotenuse^2=perpendicular^2+base^2`

`d^2=a^2+a^2`

`d^2=2a^2`

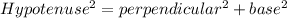
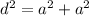
Taking square root on both sides.

`d=√(2a^2)`

`d=a√(2)`

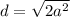
Putting a=6, we get

`d=6√(2)`

`d=6(1.414)`

`d=8.484<10`

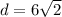
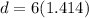
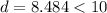
Since, the diagonal of the square is less than the diameter of the circle, therefore the square will fit inside the circle without touching the edge of the circle.

Hence proved.