Answer:
Explanation:
Let A denote the score for students of section A.
Let B denote the score for students of section B.
It is provided that:
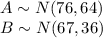
The scores of the students of the two section are independent.
Compute the mean and variance of A - B as follows:
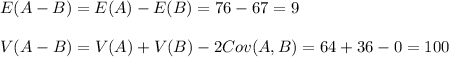
Compute the probability that the scores of two students, one in section A and one in section B, differ by no more than 1 point in absolute value as follows:
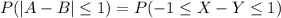
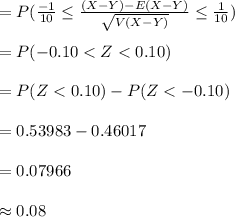
Thus, the probability that the scores of two students, one in section A and one in section B, differ by no more than 1 point in absolute value is 0.08.