Question

Determine whether the integral is convergent or divergent. 1 35 ln x x dx 0 convergent divergent Incorrect: Your answer is incorrect.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The integral is divergent

Explanation:

From the question we are told that

The equation given is

`\int\limits^(\infty)_1 {35 (ln(x))/(x) } \, dx`

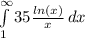
Let
`v = ln x`

=>
`(dv)/(dx) = (1)/(x)`

=>
`du = (dx)/(x)`

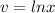
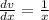
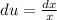
So

`\int\limits^(\infty)_1 {35 (ln(x))/(x) } \, dx = 35 \int\limits^(\infty)_1 { u} \, du`

=>
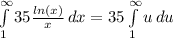
`\int\limits^(\infty)_1 {35 (ln(x))/(x) } \, dx = 35 [(u^2)/(2) ] | \left {\infty } } \atop {1}} \right.`

=>
`\int\limits^(\infty)_1 {35 (ln(x))/(x) } \, dx = (35)/(2) [(ln (x))^2] | \left {\infty } } \atop {1}} \right.`

=>
`\int\limits^(\infty)_1 {35 (ln(x))/(x) } \, dx = (35)/(2) [ [(ln (\infty))^2] - [(ln (1))^2] ]`

=>
`\int\limits^(\infty)_1 {35 (ln(x))/(x) } \, dx = (35)/(2) [ \infty - [(ln (1))^2] ]`

=>
`\int\limits^(\infty)_1 {35 (ln(x))/(x) } \, dx = (35)/(2) [ \infty ]`

=>
`\int\limits^(\infty)_1 {35 (ln(x))/(x) } \, dx = \infty`

Hence given that the solution to the integral is
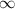`\infty` then it mean that the integral is divergent