Question

A right circular cylinder has a radius of cm and a height of cm. Use differentials to estimate the change in volume of the cylinder if its height and radius are both increased by cm. Give an exact answer.

Answer 1

The change in volume of the cylinder is 9600π cubic centimeters.

Explanation:

Statement is incomplete. Complete statement is:

A right circular cylinder has a radius of 40 cm and a height of 100 cm. Use differentials to estimate the change in volume of the cylinder if its height and radius are both increased by 1 cm.

From Geometry we know that volume of right circular cylinder, measured in cubic centimeters, is represented by the following expression:

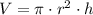`V = \pi\cdot r^(2)\cdot h` (Eq. 1)

Where:

`r` - Radius of the right circular cylinder, measured in centimeters.

`h` - Height of the right circular cylinder, measured in centimeters.

The change in volume of the cylinder, measured in cubic centimeters, is obtained by total differentials:

`\Delta V = (\partial V)/(\partial r)\cdot \Delta r + (\partial V)/(\partial h)\cdot \Delta h` (Eq. 2)

Where:

`\Delta r` - Change in radius, measured in centimeters.

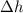`\Delta h` - Change in height, measured in centimeters.

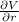`(\partial V)/(\partial r)` - Partial derivative of volume in radius, measured in square centimeters.

`(\partial V)/(\partial h)` - Partial derivative of volume in height, measured in square centimeters.

All partial derivatives are obtained, respectively:

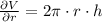`(\partial V)/(\partial r) = 2\pi\cdot r\cdot h` (Eq. 3)

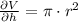`(\partial V)/(\partial h) = \pi\cdot r^(2)` (Eq. 4)

By applying (Eqs. 3, 4) in (Eq. 2), we obtain the resulting expression:

`\Delta V = 2\pi\cdot r\cdot h \cdot \Delta r+\pi\cdot r^(2)\cdot \Delta h`

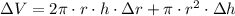
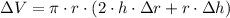`\Delta V =\pi\cdot r \cdot (2\cdot h\cdot \Delta r +r\cdot \Delta h)` (Eq. 5)

If we know that
`r = 40\,cm`,
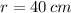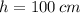`h = 100\,cm` and
`\Delta r = \Delta h = 1\,cm`, the change in volume of the cylinder is approximately:

`\Delta V = \pi\cdot (40\,cm)\cdot [2\cdot (100\,cm)\cdot (1\,cm)+(40\,cm)\cdot (1\,cm)]`

`\Delta V = 9600\pi\,cm^(3)`

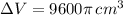
The change in volume of the cylinder is 9600π cubic centimeters.