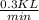Question

5 L/s = __ kL/min please show work :)

Answer 1

`the \: right \: value \: is \: 0.3kL/min`

Explanation:

`you \: can \: start \: by \: knowing \: that : \\ 1 \: (kL)/(min) = (1000L)/(60s) = (50L)/(3s) = (50)/(3) {L(s)}^( - 1) \\ so \: if \: (50)/(3) {L(s)}^( - 1) = 1 \: (kL)/(min)\\ then \\ 5 {L(s)}^( - 1) \: will \: be \: = \: \frac{1 {kL(m)}^( - 1) * 5 {L(s)}^( - 1) }{(50)/(3) {Ls}^( - 1) } \\ = 0.3{kL(m)}^( - 1)`

Answer 2

`(0.3KL)/(min)`

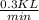
Explanation:

okay, so first, you have

`(5L)/(s)`

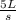
you are going to work with Liters first. you want to cancel out variables to get it to equal the specified ones, so if one liter is equal to 0.001 kl, you do:
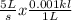`(5L)/(s) x (0.001kl)/(1L)` . you put liter on bottom because when you have L over L, it cancels out.

then work with seconds. 60 seconds are in a minute, so

`(5L)/(s) x(60s)/(min)`. you want them to cancel out, so that's why you put seconds on top.

so now, put everything together

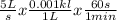`(5L)/(s) x(0.001kl)/(1L) x(60s)/(1min)` so now, multiply the stuff on the top together, and the stuff on the bottom together, and you will get your answer of

`(0.3KL)/(min)`