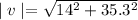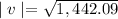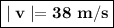Answer:
a) t=3.6 sec
b)
Step-by-step explanation:
Horizontal Motion
When an object is thrown horizontally with a speed v from a height h, it describes a curved trajectory ruled by a constant speed in the horizontal direction and a variable speed in the vertical direction, where the acceleration of gravity makes the object fall to the ground.
If we know the height h from which the object was launched, the time it takes to hit the ground is:
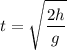
The horizontal speed is always constant:
vx=vo
But the vertical speed depends on the time and acceleration of gravity:
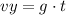
The magnitude of the velocity or final speed of the object is given by:
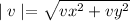
a.
The stone was kicked over the cliff with a speed of v0=14 m/s, and the height it was thrown from is h=63.5 m, thus:
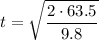
t=3.6 sec
b.
The vertical speed is:
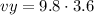
vy=35.3 m/s
The final speed is calculated below: