Question

4. A statistician working for the National Basketball Association supplies the television announcers with interesting statistics. At a certain point in the season, he discovered that in 375 games, 300 were won by the team that was winning the game at the end of the third quarter. The margin of error in a 90% confidence interval estimate of the true proportion of games won by the team leading at the end of the third quarter with the plus-4 adjustment applied is (Show work): (5)

Answer 1

Answer: 0.038

Explanation:

Given: Total games : n= 375

Number of games won by the team that was winning the game at the end of the third quarter. = 300

The proportion (p) of the team that was winning the game at the end of the third quarter:
`p=(300)/(375)=0.8`

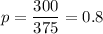
Critical z-value for 90% confidence: z* = 1.645

Margin of error =
`z^*\sqrt{((1-p)p)/(n)}`

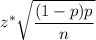
The margin of error in a 90% confidence interval estimate of p
`=1.645\sqrt{(0.2*0.8)/(300)}\\= 1.645*√(0.00053333)\\\\=1.645*0.0231\\\\=0.0379995\approx$$0.038`

Hence, the required margin of error = 0.038