Question

Which values of x and y would make the following expression represent a real number? (4+5i)(x+ yi)

Ox=4,y= 5
Ox=-4, y = 0
Ox=4, y=-5
Ox=0, y= 5​

Answer 1

c

Explanation:

Answer 2

C

Explanation:

We have the expression
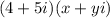`(4+5i)(x+yi)` and we want to find the values of
`x` and
`y` such that the expression will evaluate to a real number.

So, let's first expand the expression. Distribute:

`=4(x+yi)+5i(x+yi)`

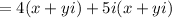
Distribute:

`=4x+4yi+5xi+5yi^2`

Simplify:

`=(4x-5y)+(4yi+5xi)`

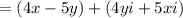
So, we want to make the second part within the real numbers.

Notice that we only have two ways of doing this: 1) Either both
`x` and
`y` are imaginary numbers themselves canceling out the
`i`, or 2), the entire expression equals 0.

Since our answer choices consists of only real numbers, this means that the imaginary part must be equal to 0. So:

`4yi+5xi=0`

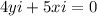
We can divide everything by
`i`:

`4y+5x=0`

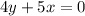
Now, we can use our answer choices.

Running down the list, we can see that the choice that works is C. If we substitute the values of C into the equation, we get:

`4(-5)+5(4)=0\\\Rightarrow -20+20=0\stackrel{\checkmark}{=}0`

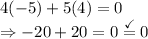
Therefore, our answer is C.