Question

Given that measure OAB equals 45. What is the area of the shaded portion of the circle?

Answer 1

D.
`8\pi-16`

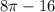
Explanation:

A circle measures 360 degrees and has an area
`A=\pi{r}^2`

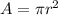
The radius (also side length) is given:
`4√(2)`.

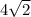The area of this circle is
`A=\pi\cdot{4}{√(2)}^2=32\pi`

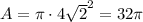
The area of a triangle is (1/2)bh, so this triangle is:
`((1)/(2))\cdot 4√(2)\cdot4√(2)=A`

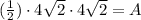
Triangle area: A = 16 units^2.

• This is a right triangle that's also a 45, 45, 90 triangle. In these special triangles, the side lengths (AO and OB) will be the same. It also means the hypotenuse is such side length times the sqrt of 2.

Now, subtract the area of the triangle from 1/4 of the circle's area:

(1/4)32pi - 16 = 8pi - 16