Question

ES 1. How fast must a truck travel to stay beneath an airplane that is moving 105 km/hr at an angle of 25 degrees to the ground?​

Answer 1

The truck must travel at a speed of 98.6677 km/hr to stay beneath the airplane

Step-by-step explanation:

The given parameters are;

The velocity of the airplane, v = 105 km/hr

The direction of the airplane, θ = 25 degrees to the ground = 25°

Therefore, we have that the horizontal component of the velocity of the plane, vₓ is given as follows;

vₓ = v × cos(θ) = 105 km/hr × cos(25) ≈ 98.6677 km/hr

The vertical component of the velocity of the plane,
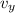`v_y`, is given as follows;

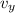`v_y` = v × sin(θ) = 105 km/hr × sin(25) ≈ 44.37 km/hr

The truck only has to travel at a speed equal to the horizontal velocity of the airplane to stay beneath the airplane

Therefore, the travelling speed the truck must be vₓ which is 98.6677 km/hr to stay beneath the airplane.