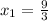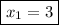Answer:
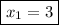

Explanation:
Solve the following equation:
![\left[\begin{array}{ccc}3&2\\5&5\\\end{array}\right] \left[\begin{array}{ccc}x_(1)\\x_(2)\\\end{array}\right] + \left[\begin{array}{ccc}1\\2\\\end{array}\right] = \left[\begin{array}{ccc}2\\-3\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ji6pqgs3wtmxvvbo56ejeqc9yypvxytvoo.png)
-In order to solve a pair of equations by using substitution, you first need to solve one of the equations for one of variables and then you would substitute the result for that variable in the other equation:
-First equation:
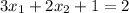
-Second equation:

-Choose one of the two following equations, which I choose the first one, then you solve for
 by isolating
by isolating
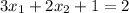
-Subtract
 to both sides:
to both sides:
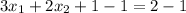

-Subtract
 to both sides:
to both sides:

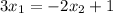
-Divide both sides by
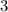 :
:
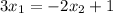

-Multiply
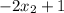 by
by
 :
:

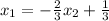
-Substitute
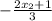 for
for
 in the second equation, which is
in the second equation, which is
 :
:


Multiply
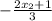 by
by
 :
:


-Combine like terms:

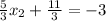
-Subtract
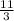 to both sides:
to both sides:

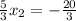
-Multiply both sides by
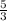 :
:
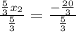

-After you have the value of
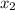 , substitute for
, substitute for
 onto this equation, which is
onto this equation, which is
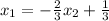 :
:
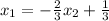
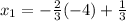
-Multiply
 and
and
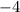 :
:
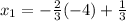

-Since both
 and
and
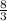 have the same denominator, then add the numerators together. Also, after you have added both numerators together, reduce the fraction to the lowest term:
have the same denominator, then add the numerators together. Also, after you have added both numerators together, reduce the fraction to the lowest term: