Answer: "
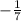 " .
" .
_____________
Explanation:
Assume we have a two-dimension Cartesian plane graph;
in which equations of straight lines can be expressed in the form of:
" y = mx + b " ;
in which:
"m" is the slope; as well as the "coefficient" of "x" ;
and: "b" is the y-intercept; that is, the value "y" value of the "(x, y)" coordinate at the point which "x = 0" ; that is, where the graph crosses the "y-axis".
Given the ^aformentioned conditions:
Note that if we select a line that can be written in the format:
" y = mx + b " ; then another line that is "perpendicular" to that
[selected line] will have the slope, "m"; of the value that is the "negative reciprocal value" of the slope, "m" ; of the other line.
Note that is our problem, we select a line—in our given problem:
"Line a" —with a slope, "m = 7 " ;
which is perpendicular to the slope of "Line b" ;
→ then: the slope of "Line B" ; would be the "negative reciprocal value"
of "7" .
Note: "
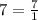 " ; the recriprocal would be: "
" ; the recriprocal would be: "
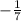 " .
" .
_____________
Hope this answer is helpful to you!