Question

Certain answers please, I raised it ;)

Answer 1

Hello!!! Princess Sakura here ^^

Explanation:

a) p=1/2

b) 25

Answer 2

1) p=1/2

2) V(p)=25

Explanation:

We have the function:

`V(p)=100p(1-p)`

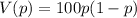
Which represents the variance of the number of left handed people in a group of 100.

Question 1)

We want to find the value of p that maximizes the variance.

Let's examine our function. We can see that it is a quadratic. Therefore, the value of p that maximizes the variance will simply be the x-coordinate of the vertex of our equation.

Let's expand our function:

`V(p)=100p(1-p)`

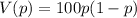
Distribute:

`V(p)=100p-100p^2`

Let's find the vertex of our equation. We can use the following formulas (I switched out the x for p):

`p=-b/2a,\ V(-b/2a)`

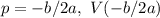
Let's determine our coefficients. The "a" is the coefficient in front of the squared term and "b" is the coefficient in front of the x term.

So, a is -100, and b is 100.

Substitute them into our formula:

`p=-(100)/2(-100)`

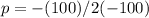
Multiply:

`p=100/200`

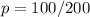
Divide:

`p=1/2`

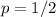
So, the x-coordinate (or rather p in this case) of our vertex is 1/2.

To find the y-value, let's substitute it back into our function. We have:

`V(p)=100p-100p^2`

Substitute 1/2 for p:

`V(1/2)=100(1/2)-100(1/2)^2`

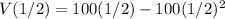
Evaluate:

`V(1/2)=50-25=25`

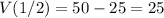
Therefore, our vertex is:

`(1/2, 25)`

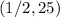
So, the value of p that maximizes our variance is p=1/2.

Question 2)

We want to find the maximum variance.

Again, this will simply be the vertex of our quadratic.

This time, it will be the y-coordinate.

We can see that the y-coordinate of the vertex is 25.

So, our maximum variance is V(p)=25.

And we're done!