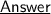
The value that satisfies the first degree equation is: x = 2.
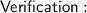
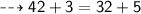
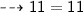
Solving a first degree equation
The objective of the problem is to know what is the number that allows the stated equality to be fulfilled, for this it is necessary to clear the value of x.
The formulation is first degree:
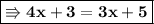
The variables must be grouped in the same term, in this case we will do it in the left term, and the constants (numbers) in the right.
1) Subtract -3x from both terms:
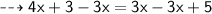
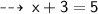
2) Subtract three units for each term:

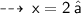
I hope I've helped : )