Question

1. Carter will install fencing all around the flat area of his

backyard. Determine the amount of fencing he needs to the
nearest whole yard,

Answer 1

75 yards

Explanation:

Answer 2

Amount of fencing required = 75 yards

Explanation:

Distance between the two points
`(x_1,y_1)` and
`(x_2,y_2)` is given by the formula,

d =
`√((x_2-x_1)^2+(y_2-y_1)^2)`

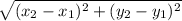
Distance between A(3, 6) and B(3, -2) =
`√((3-3)^2+(6+2)^2)`

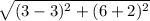
= 8 yards

Distance between B(3, -2) and C(-7, 4) =
`√((3+7)^2+(-2-4)^2)`

=
`√(136)`

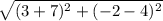
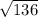
= 11.66 ≈ 12 yards

Distance between C(-7, 4) and D(-7, -2) =
`√((-7+7)^2+(4+2)^2)`

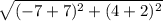
= 6 yards

Distance between D(-7, -2) and E(-3, -2) =
`√((-7+3)^2+(-2+2)^2)`

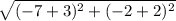
= 4 yards

Distance between E(-3, -2) and F(-3, -8) =
`√((-3+3)^2+(-2+8)^2)`

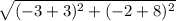
= 6 yards

Distance between F(-3, -8) and G(3, -8) =
`√((-3-3)^2+(-8+8)^2)`

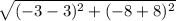
= 6 yards

Distance between G(3, -8) and H(10, -12) =
`√((3-10)^2+(-8+12)^2)`

=
`√(49+16)`

=
`√(65)`

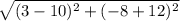
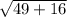
= 8.06 ≈ 8 yards

Distance between H(10, -12) and J(10, 6) =
`√((10-10)^2+(-12-6)^2)`

= 18 yards

Distance between A(3, 6) and J(10, 6) =
`√((10-3)^2+(6-6)^2)`

= 7 yards

Since length of fence required = perimeter of the flat area

Perimeter of the given area = 8 + 12 + 6 + 4 + 6 + 6 + 8 + 18 + 7

= 75 yards

Therefore, amount of fencing required = 75 yards