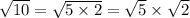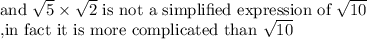Answer:
true
Explanation:
Examples :
180 = 5 × 2² × 3²
Then
The number 180 has perfect square factors which are 2 and 3
Then
The number √180 can be simplified because:
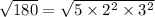
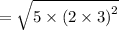



On the other hand :
10 = 5 × 2
Then
The number 10 has no perfect square factors
Then
The number √10 cannot be simplified because: