Question

1. You work with traffic engineers for DOT (the department of transportation) and is in charge of performing measurements and analyzing speeding on a busy road. After measuring the speeds and collected a very large data sample, the speed on that road was found to have a Gaussian distribution with an average of 67 mph and standard deviation of 4 mph. If the highway patrol plans to ticket anyone driving faster than 72 mph, what is the % of drivers that will exceed this limit?

Answer 1

The % of drivers that will exceed this limit is 10.56 %

Explanation:

Let's start defining the random variable :

`X` : '' The speed on that road ''

We know that
`X` can be modeled with a Gaussian distribution ⇒

`X` ~
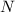`N` ( μ , σ )

Where ''μ'' is the mean and ''σ'' is the standard deviation. Given that the average speed and the standard deviation of the problem are known we write :

`X` ~
`N(67,4)`

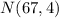
We are asked about
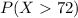`P(X>72)` (which is the % of drivers that will exceed this limit).

To find this probability we are going to make a standardization of the variable
`X` (also called a change of variables).

We are going to substract the mean to
`X` and then divide by its standard deviation :

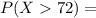`P(X>72)=` P [(X-μ) / σ > (72 - μ) / σ] (I)

The new variable [(X - μ) / σ] is called Z.

Z can be modeled as

`Z` ~
`N(0,1)`

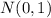
⇒ Replacing in (I) the values of the mean and the standard deviation :

`P(Z>(72-67)/(4))` =
`P(Z>1.25)=1-P(Z\leq 1.25)`

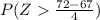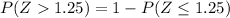
The convenience of this is that we can find the probabilities of Z (which is a N(0,1) ) in any table on internet ⇒

Looking at any table we will find that
`P(Z\leq 1.25)=0.8944` ⇒

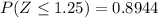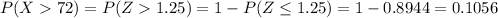`P(X>72)=P(Z>1.25)=1-P(Z\leq 1.25)=1-0.8944=0.1056` = 10.56 %

We find that the % of drivers that will exceed this limits is 10.56 %