Answer: 0.07938
Explanation:
Let X be a binomial variable that represents the components of a specific engine.
As per given , the probability of componentis found to not perform to standards : p= 1%=0.01
Binomial probability formula :
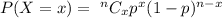
Sample size : n= 100
If more than two are found to be non-performing the entire shipment is returned.
Now, Required probability :
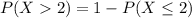
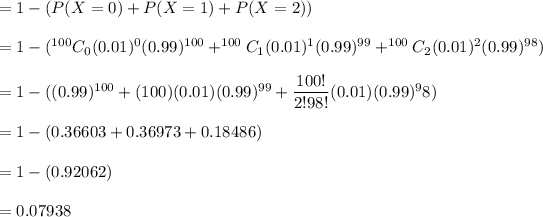
So, the probability that a shipment is returned = 0.07938