Question

Whats the answer to that question?

Answer 1

-0.9090... can be written as
`(10)/(11)`.

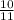Step-by-step explanation:

Any repeating decimal can be written as a fraction by dividing the section of the pattern to be repeated by 9's.

We can start by listing out

0.909090... = 9/10 + 0/100 + 9/1000 + 0/10000 + 9/100000 + 0/1000000 + ...

Now. we let this series be equal to x, that is

`x` = 9/10 + 0/100 + 9/1000 + 0/10000 + 9/100000 + 0/1000000 + ...

Now, we'll multiply both sides by 100 .

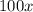`100x` = 90 + 0 + 9/10 + 0/100 + 9/1000 + 0/10000 + ...

Then, subtract the 1st equation from the second like so:

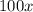`100x` = 90 + 0 + 9/10 + 0/100 + 9/1000 + 0/10000 + 9/100000 + 0/1000000 + ...

`-x` = - 9/10 - 0/100 - 9/1000 - 0/10000 - 9/100000 - 0/1000000 - ...

And we end up with this:

`99x=90`

Finally, we divide both sides by 99 in order to isolate x and get the fraction we're looking for.

`x=(90)/(99)`

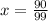
Which can be reduced and simplified to

`x=(10)/(11)`

Hope this helps!