Question

Express w as a linear combination of the vector V1 and V2 if this is possible. If not, Show that it is impossible.

w= [3]
[-1]
[2]

v1= [-3]
[1]
[2]

v2= [6]
[-2]
[3]

Answer 1

Explanation:

`w=((1)/(7)).V_(1)+((4)/(7)).V_(2)`

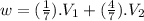
We have the following vectors :

`w=\left[\begin{array}{c}3&-1&2\end{array}\right]`

`V_(1)=\left[\begin{array}{c}-3&1&2\end{array}\right]`

`V_(2)=\left[\begin{array}{c}6&-2&3\end{array}\right]`

In order to express
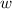`w` as a linear combination of the vectors
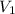`V_(1)` and
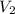`V_(2)`, we will search for
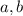`a,b` ∈ IR such that :

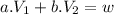`a.V_(1)+b.V_(2)=w` (I)

Now we are going to work matrixically with the equation (I) :

`a\left[\begin{array}{c}-3&1&2\end{array}\right]+b\left[\begin{array}{c}6&-2&3\end{array}\right]=\left[\begin{array}{c}3&-1&2\end{array}\right]`

Distributing mathematically and matching ''component to component'' we lead to the following equations :

`-3a+6b=3\\a-2b=-1\\2a+3b=2`

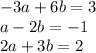
Working with the system associated matrix :

`\left[\begin{array}{ccc}-3&6&3\\1&-2&-1\\2&3&2\end{array}\right]`

Applying matrix operations we lead to the following equivalent matrix :

`\left[\begin{array}{ccc}1&0&(1)/(7)\\0&1&(4)/(7)\\0&0&0\end{array}\right]`

In this matrix we obtain that :

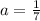`a=(1)/(7)` and
`b=(4)/(7)`

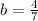
We can verify this solution by replacing the values of
`a` and
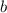`b` in the equation (I) :

`((1)/(7)).V_(1)+((4)/(7)).V_(2)=w` ⇒

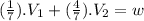`((1)/(7)).\left[\begin{array}{c}-3&1&2\end{array}\right]+((4)/(7)).\left[\begin{array}{c}6&-2&3\end{array}\right]=\left[\begin{array}{c}3&-1&2\end{array}\right]` ⇒

`\left[\begin{array}{c}3&-1&2\end{array}\right]=\left[\begin{array}{c}3&-1&2\end{array}\right]`