Answer:
Zeroes : 1, 4 and -5.
Potential roots:
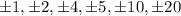 .
.
Explanation:
The given equation is

It can be written as
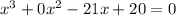
Splitting the middle terms, we get
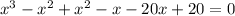
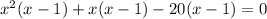
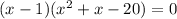
Splitting the middle terms, we get
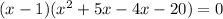
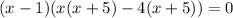
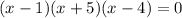
Using zero product property, we get

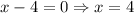
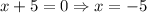
Therefore, the zeroes of the equation are 1, 4 and -5.
According to rational root theorem, the potential root of the polynomial are
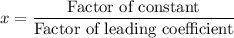
Constant = 20
Factors of constant ±1, ±2, ±4, ±5, ±10, ±20.
Leading coefficient= 1
Factors of leading coefficient ±1.
Therefore, the potential root of the polynomial are
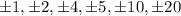 .
.