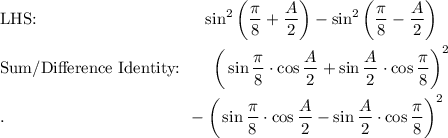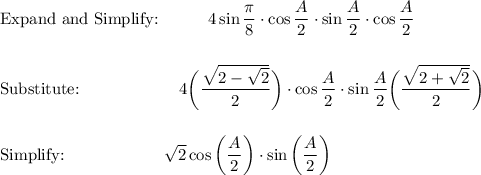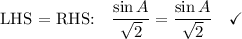Question

Please prove this!!!!​

Answer 1

Answer: see proof below

Explanation:

Use the following Sum/Difference Identities:

sin(A + B) = sin A · cos B + sin B · cos A

sin(A - B) = sin A · cos B - sin B · cos A

Use the following Half-Angle Identities:

`\sin\bigg((\theta)/(2)\bigg)=(√(1-\cos \theta))/(\sqrt2)\\\\\\\cos\bigg((\theta)/(2)\bigg)=(√(1+\cos \theta))/(\sqrt2)`

`\text{Use the Unit circle to evaluate:}\ \cos(\pi)/(4) = \sin(\pi)/(4) = (\sqrt2)/(2)`

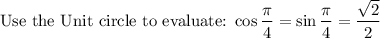
Use the following side work:

`\sin\bigg((\pi)/(8)\bigg)=\sin\bigg(((\pi)/(4))/(2)\bigg)=\frac{\sqrt{1-\cos (\pi)/(4)}}{\sqrt2}=(√(2-\sqrt2))/(2)\\\\\\\cos\bigg((\pi)/(8)\bigg)=\cos\bigg(((\pi)/(4))/(2)\bigg)=\frac{\sqrt{1+\cos (\pi)/(4)}}{\sqrt2}=(√(2+\sqrt2))/(2)`

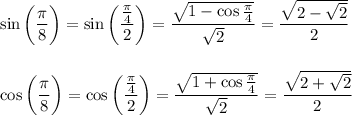
Proof LHS → RHS

`\text{LHS:}\qquad \qquad \qquad \qquad \qquad \sin^2\bigg((\pi)/(8)+(A)/(2)\bigg)-\sin^2\bigg((\pi)/(8)-(A)/(2)\bigg)\\\\\text{Sum/Difference Identity:}\qquad \bigg(\sin(\pi)/(8)\cdot \cos (A)/(2)+\sin (A)/(2)\cdot \cos (\pi)/(8)\bigg)^2\\\\.\qquad \qquad \qquad\qquad \qquad \quad -\bigg(\sin(\pi)/(8)\cdot \cos (A)/(2)-\sin (A)/(2)\cdot \cos (\pi)/(8)\bigg)^2`

`\text{Expand and Simplify:}\qquad \quad 4\sin (\pi)/(8)\cdot \cos(A)/(2)\cdot \sin (A)/(2)\cdot \cos (A)/(2)\\\\\\\text{Substitute:}\qquad \qquad \qquad 4\bigg((√(2-\sqrt2))/(2)\bigg)\cdot \cos (A)/(2)\cdot \sin (A)/(2)\bigg((√(2+\sqrt2))/(2)\bigg)\\\\\\\text{Simplify:}\qquad \qquad \qquad \sqrt2\cos \bigg((A)/(2)\bigg)\cdot \sin \bigg((A)/(2)\bigg)`

`\text{Half-Angle Identity:} \quad \sqrt2\bigg((√(1+\cos A))/(\sqrt2)\bigg)\bigg((√(1-\cos A))/(\sqrt2)\bigg)\\\\\\\text{Simplify:}\qquad \qquad \qquad (√(1-\cos^2 A))/(\sqrt2)\\\\\\.\qquad \qquad \qquad \qquad =(√(\sin^2 A))/(\sqrt2)\\\\\\.\qquad \qquad \qquad \qquad =(\sin A)/(\sqrt2)`

`\text{LHS = RHS:}\quad (\sin A)/(\sqrt2) = (\sin A)/(\sqrt2)\quad \checkmark`