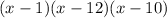Question

Factorise x 3 - 2 3 x 2 + 142x - 120????​

Answer 1

`(x - 1)(x - 12)(x - 10)`

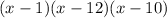
Explanation:

Given

Factorize:

`x^3 - 23x^2 + 142x - 120`

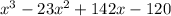
Required

Factorize

We start by checking for the factors of the given polynomial;

Check x - 1 = 0;

This implies that x = 1

Substitute 1 for x in
`x^3 - 23x^2 + 142x - 120`

`(1)^3 - 23(1)^2 + 142(1) - 120`

`= 1 - 23 + 142 - 120`

`= 0`

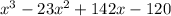
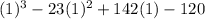
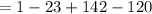
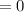
Since the result is 0, then x - 1 = 0 is a factor

Divide the polynomial by x - 1

(See attachment for long division)

The result is:
`x^2 - 22x + 120`

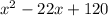
Hence, the factor is

`(x - 1)(x^2 - 22x + 120)`

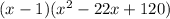
Expand the quadratic function

`(x - 1)(x^2 - 12x - 10x + 120)`

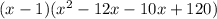
Factorize

`(x - 1)(x(x - 12) - 10(x - 12))`

`(x - 1)(x - 12)(x - 10)`

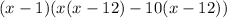
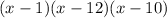
Hence;

Factorizing
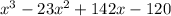`x^3 - 23x^2 + 142x - 120` gives
`(x - 1)(x - 12)(x - 10)`