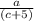Answer:
d = 55.5
x = 1
c = 11
m =
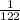
k =
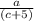
Explanation:
Sorry, the formatting is slightly hard to understand, but I think this is what you meant.
Q1.
 d - 8 =
d - 8 =
 x 2
x 2
Step 1. Simplify.
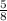 x 2 =
x 2 =
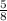 x
x
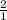 =
=
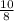
Step 2. Cancel out the negative 8.
 d - 8 =
d - 8 =
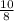
+ 8 to both sides (do the opposite:
 d is subtracting 8 right now, but to cancel that out, we will do the opposite of subtraction, i.e. addition)
d is subtracting 8 right now, but to cancel that out, we will do the opposite of subtraction, i.e. addition)
 d =
d =
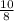 + 8
+ 8
Step 3. Simplify.
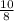 + 8 =
+ 8 =
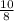 +
+
 =
=
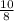 +
+
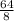 =
=
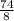 =
=
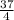
Step 4. Cancel out the
 .
.
 d =
d =
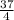
÷
 from both sides (do the opposite: d is multiplied by
from both sides (do the opposite: d is multiplied by
 right now, but to cancel that out, we will do the opposite of multiplication, i.e. division)
right now, but to cancel that out, we will do the opposite of multiplication, i.e. division)
÷
 = x 6
= x 6
So....
x 6 to both sides
d =
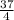 x 6 =
x 6 =
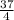 x
x
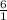 =
=
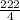 =
=
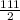 = 55.5
= 55.5
Step 5. Write down your answer.
d = 55.5
Q2.
3x - 4 + 5x = 10 - 2x × 3
Step 1. Simplify
3x - 4 + 5x = 3x + 5x - 4 = 8x - 4
10 - 2x × 3 = 10 - (2x × 3) = 10 - 6x
Step 2. Cancel out the negative 6x
8x - 4 = 10 - 6x
+ 6x to both sides (do the opposite - you're probably tired of reading this now - right now it's 10 subtract 6x, but the opposite of subtraction is addition)
14x - 4 = 10
Step 3. Cancel out the negative 4
14x - 4 = 10
+ 4 to both sides (right now it's 14x subtract 4, but the opposite of subtraction is addition)
14x = 14
Step 4. Divide by 14
14x = 14
÷ 14 from both sides (out of the [14 × x] we only want the [x], so we cancel out the [× 14])
x = 1
Step 5. Write down your answer.
x = 1
Q3.
7(c - 3) = 14 × 4
Step 1. Expand the brackets
7(c - 3) = (7 x c) - (7 x 3) = 7c - 21
Step 2. Simplify
14 x 4 = 56
Step 3. Cancel out the negative 21
7c - 21 = 56
+ 21
7c = 56 + 21
7c = 77
Step 4. Cancel out the ×7
7c = 77
÷ 7
c = 77 ÷ 7
c = 11
Step 5. Write down your answer.
c = 11
Q4.
11(
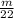 +
+
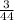 ) = 87m + m × 5
) = 87m + m × 5
Step 1. Expand the brackets
11(
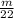 +
+
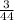 ) = (11 x
) = (11 x
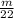 ) + (11 x
) + (11 x
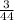 ) = (
) = (
 x
x
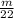 ) + (
) + (
 x
x
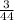 ) =
) =
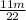 +
+
 =
=
 +
+

Step 2. Simplify.
87m + m x 5 = 87m + 5m = 92m
Step 3. Cancel out the add

 +
+
 = 92m
= 92m
-

 = 92m -
= 92m -

 =
=
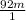 -
-

 =
=
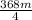 -
-

 =
=
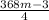
Step 4. Cancel out the ÷ 4
 =
=
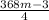
x 4
2m = 368m - 3
Step 5. Cancel out the 368m
2m = 368m - 3
- 368m
-366m = - 3
Step 6. Cancel out the × -366
-366m = -3
÷ -366
m =
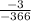
m =
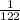
Step 7. Write down your answer.
m =
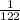
Q5.
ck + 5k = a
Step 1. Factorise
ck + 5k = (c × k) + (5 × k) = (c + 5) x k = k(c + 5)
Step 2. Cancel out the × (c + 5)
k(c + 5) = a
÷ (c + 5)
k = a ÷ (c + 5)
k =