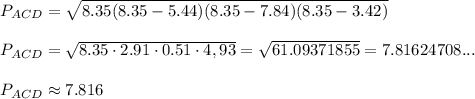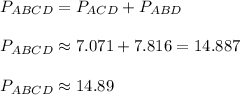Question

Find the area of quadrilateral ABCD.

Answer 1

14.89 units²

Explanation:

`P_(ABCD)=P_(ACD)+P_(ABD)`

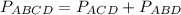
We can use Heron's formula to calculate area of triangles:

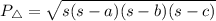`P_\triangle=√(s(s-a)(s-b)(s-c))` where:

a, b, c - sides of triangle

s - semi-perimetr of triangle {(a+b+c):2}

ΔACD:

a = 4.39 , b = 3.42 , c = 4.57

s = (4.39 + 3.42 + 4.57)÷2 = 12.38÷2 = 6.19

`P_(ACD)=√(6.19(6.19-4.39)(6.19-3.42)(6.19-4.57))\\\\P_(ACD)=√(6.19\cdot1.8\cdot2.77\cdot1.62)=√(49.9986108)=7.070969579...\\\\P_(ACD)\approx7.071`

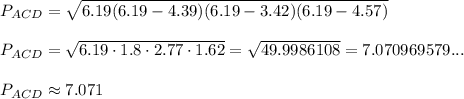
ΔACD:

a = 5.44 , b = 7.84 , c = 3.42

s = (5.44 + 7.84 + 3.42)÷2 = 16.7÷2 =
`P_(ACD)=√(8.35(8.35-5.44)(8.35-7.84)(8.35-3.42))\\\\P_(ACD)=√(8.35\cdot2.91\cdot0.51\cdot4,93)=√(61.09371855)=7.81624708...\\\\P_(ACD)\approx7.816`

`P_(ABCD)=P_(ACD)+P_(ABD)\\\\P_(ABCD)\approx7.071+7.816 = 14.887\\\\P_(ABCD)\approx 14.89`

Answer 2

The correct answer is B. 14.89 units squared.

Find the area of each triangle and add them together. Heron’s formula explains it better than me. Lol