Question

Fill in the blank with a constant, so that the resulting quadratic expression is the square of a binomial. $\[x^2 + 22x + \underline{~~~~}.\]$

Answer 1

The answer would be x^2+22x+121

Answer 2

`$\[x^2 + 22x + 121\]$`

Explanation:

Given

`$\[x^2 + 22x + \underline{~~~~}.\]$`

Required

Fill in the gap

Represent the blank with k

`$\[x^2 + 22x + k\]$`

Solving for k...

To do this, we start by getting the coefficient of x

Coefficient of x = 22

Divide the coefficient by 2

`Result = 22/2`

`Result = 11`

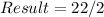
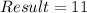
Take the square of this result, to give k

`k= 11^2`

`k= 121`

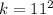
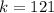
Substitute 121 for k

`$\[x^2 + 22x + 121\]$`

The expression can be factorized as follows;

`x^2 + 11x + 11x + 121`

`x(x + 11)+11(x+11)`

`(x+11)(x+11)`

`(x+11)^2`

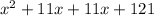
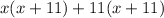
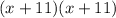
Hence, the quadratic expression is
`$\[x^2 + 22x + 121\]$`