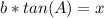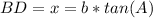Question

In terms of the trigonometric ratios for ΔABD, what is the length of line segment BD?

Answer 1

In terms of the trigonometric ratios for ΔABD, what is the length of line segment BD?

Answer:

`BD = c*sin(A)`

`BD = c*cos(B)`

`BD = b*tan(A)`

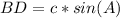
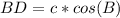
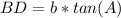
Explanation:

∆ABD is a right triangle.

Recall: trigonometric ratios of any right triangle can easily be understood or remembered with the acronym, SOHCAHTOA.

SOH => sin(θ) = opposite/hypotenuse

CAH => Cos(θ) = adjacent/hypotenuse

TOA = tan(θ) = opposite/adjacent

Thus, the length of segment BD, in terms of trigonometric ratios for ∆ABD can be done as follows:

Let BD = x

AB = c

AD = b

=>The sine ratio for the length of line segment BD = x, using SOH.

θ = A

Opposite = DB = x

hypotenuse = AB = c

`sin(A) = (x)/(c)`

Make x the subject of formula.

`c*sin(A) = x`

`BD = x = c*sin(A)`

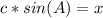
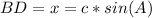
=>The Cosine ratio for the length of line segment BD = x, using CAH

θ = B

Adjacent = DB = x

hypotenuse = AB = c

`cos(B) = (x)/(c)`

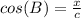
Make x the subject of formula.

`c*cos(B) = x`

`BD = x = c*cos(B)`

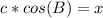
=>The Tangent ratio for the length of line segment BD = x, using TOA

θ = A

Adjacent = DB = x

hypotenuse = AD = b

`tan(A) = (x)/(b)`

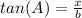
Make x the subject of formula.

`b*tan(A) = x`

`BD = x = b*tan(A)`