Question

Given the set of data: 24, 43, 65, 12, 31, 78, 43, 24, 25, 18, 29, 53, 18, 23, 20, 43, 53, 25 a. Find the mode. b. Find the median. c. Find the mean, to the nearest tenth. d. Find the midrange. e. Find the standard deviation, to the nearest hundredth. f. Determine the quartiles.

Answer 1

Answer: a. 43

b. 27

c. 34.8

d. 45

e. 17.72

f. First quartile = 23

Second quartile = 27

Third quartile =43

Explanation:

The given set of data: 24, 43, 65, 12, 31, 78, 43, 24, 25, 18, 29, 53, 18, 23, 20, 43, 53, 25

Arrange in Ascending order:

12 ,18,18 , 20 ,23 ,24 , 24 ,25 , 25 , 29, 31, 43, 43 , 43 , 53 , 53, 65 , 78

Total data points: n= 18 ( even)

a. Mode= Most repeated data value = 43

i.e. mode =43

b. Median =
`\frac{((n)/(2))^(th)\text{term}+((n)/(2)+1)^(th)\text{term}}{2}`

`=\frac{((18)/(2))^(th)\text{term}+((18)/(2)+1)^(th)\text{term}}{2}\\\\=\frac{9^(th)\text{term}+10^(th)\text{term}}{2}\\\\=(25+29)/(2)\\\\=27`

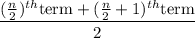
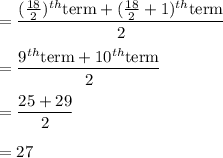
i.e. median = 27

c. Mean = (sum of data points)÷n

Sum =12+18+18 + 20 +23 +24 + 24 +25 + 25 + 29+ 31+ 43+ 43 + 43 + 53 + 53+ 65 + 78=627

Mean = 627 ÷ 18 ≈34.8

i.e. Mean = 34.8

d. Mid range =
`\frac{\text{Maximum value +Minimum value}}{2}`

`=(78+12)/(2)\\\\=(90)/(2)\\\\=45`

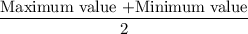
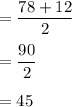
e. Standard deviation =
`\sqrt{(\sum (x-mean)^2)/(n)}`
`\sum (x-\mean)^2=(12-34.8)^2+(18-34.8)^2+(18 -34.8)^2+( 20 -34.8)^2+(23 -34.8)^2+(24 -34.8)^2+( 24 -34.8)^2+(25 -34.8)^2+2( 25 -34.8)^2+( 29-34.8)^2+( 31-34.8)^2+( 43-34.8)^2+( 43 -34.8)^2+( 43 -34.8)^2+( 53 -34.8)^2+( 53-34.8)^2+( 65 -34.8)^2+( 78-34.8)^2\\\\=5654.56`

`\sqrt{(5654.56)/(18)}=√(314.1422)\approx17.72`

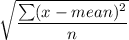
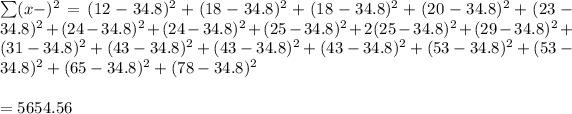
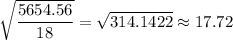
f. First quartile = Median of first half (12 ,18,18 , 20 ,23 ,24 , 24 ,25 , 25)

= 23 (middle most value)

Second quartile = Median = 27

Third quartile = Median of second half (29, 31, 43, 43 , 43 , 53 , 53, 65 , 78)

= 43 (middle most value)