Question

The Airline Passenger Association studied the relationship between the number of passengers on a particular flight and the cost of the flight. It seems logical that more passengers on the flight will result in more weight and more luggage, which in turn will result in higher fuel costs. For a sample of 21 flights, the correlation between the number of passengers and total fuel cost was 0.668.

(1)
State the decision rule for 0.10 significance level: H0: Ï â‰¤ 0; H1: Ï > 0 (Round your answer to 3 decimal places.)


Reject H0 if t >
(2)
Compute the value of the test statistic. (Round your answer to 3 decimal places.)


Value of the test statistic

Answer 1

Decision Rule: To reject the null hypothesis if t > 1.328

t = 3.913

Explanation:

The summary of the given statistics include:

sample size n = 21

the correlation between the number of passengers and total fuel cost r = 0.668

(1) We are tasked to state the decision rule for 0.10 significance level

The degree of freedom df = n - 1

degree of freedom df = 21 - 1

degree of freedom df = 19

The null and the alternative hypothesis can be computed as:

`H_o : \rho < 0\\ \\ Ha : \rho > 0`

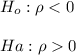
The critical value for
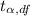`t_(\alpha, df)` is
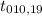`t_(010, 19)` = 1.328

Decision Rule: To reject the null hypothesis if t > 1.328

The test statistics can be computed as follows by using the formula for t-test for Pearson Correlation:

`t = r*\sqrt{ ((n-2))/((1-r^2))`

`t = 0.668*\sqrt{ ((21-2))/((1-0.668^2))`

`t = 0.668*\sqrt{ ((19))/((1-0.446224))`

`t = 0.668*\sqrt{ ((19))/((0.553776))`

`t = 0.668*5.858`

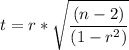
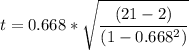
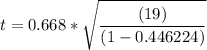
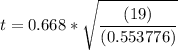
t = 3.913144

t = 3.913 to 3 decimal places