Question

When deriving the quadratic formula by completing the square, what expression can be added to both sides of the equation to create a perfect square trinomial?

Answer 1

Answer: D

Explanation:

EDGE 2023

Answer 2

According to steps 2 and 4. The second-order polynomial must be added by
`-c` and
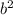`b^(2)` to create a perfect square trinomial.

Explanation:

Let consider a second-order polynomial of the form
`a\cdot x^(2) + b\cdot x + c = 0`,
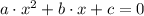`\forall \,x \in\mathbb{R}`. The procedure is presented below:

1)
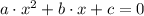`a\cdot x^(2) + b\cdot x + c = 0` (Given)

2)
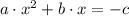`a\cdot x^(2) + b \cdot x = -c` (Compatibility with addition/Existence of additive inverse/Modulative property)

3)
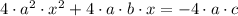`4\cdot a^(2)\cdot x^(2) + 4\cdot a \cdot b \cdot x = -4\cdot a \cdot c` (Compatibility with multiplication)

4)
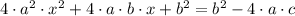`4\cdot a^(2)\cdot x^(2) + 4\cdot a \cdot b \cdot x + b^(2) = b^(2)-4\cdot a \cdot c` (Compatibility with addition/Existence of additive inverse/Modulative property)

5)
`(2\cdot a \cdot x + b)^(2) = b^(2)-4\cdot a \cdot c` (Perfect square trinomial)

According to steps 2 and 4. The second-order polynomial must be added by
`-c` and
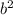`b^(2)` to create a perfect square trinomial.