Answer:
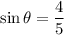 if
if
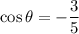 and
and
 is in the second quadrant.
is in the second quadrant.
Explanation:
By the Pythagorean Trigonometric Identity:
 for all real
for all real
 values.
values.
In this question:
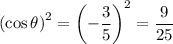 .
.
Therefore:
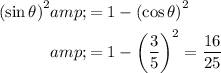 .
.
Note, that depending on
 , the sign
, the sign
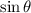 can either be positive or negative. The sine of any angles above the
can either be positive or negative. The sine of any angles above the
 axis should be positive. That region includes the first quadrant, the positive
axis should be positive. That region includes the first quadrant, the positive
 -axis, and the second quadrant.
-axis, and the second quadrant.
According to this question, the
 here is in the second quadrant of the cartesian plane, which is indeed above the
here is in the second quadrant of the cartesian plane, which is indeed above the
 -axis. As a result, the sine of this
-axis. As a result, the sine of this
It was already found (using the Pythagorean Trigonometric Identity) that:
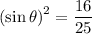 .
.
Take the positive square root of both sides to find the value of
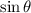 :
:
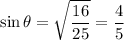 .
.